- 全部分类/
- 科学普及/
- 爆炸与冲击
 扫码免费借阅
扫码免费借阅
目录
快速导航-

研究综述 | 固体介质中的冲击极化效应研究进展
研究综述 | 固体介质中的冲击极化效应研究进展
-
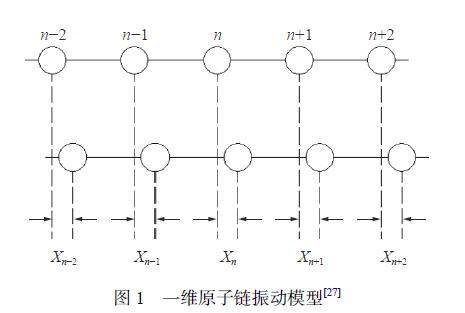
波动理论 | 基于Tersoff 势的晶格中波动传播
波动理论 | 基于Tersoff 势的晶格中波动传播
-

波动理论 | 细观非连续介质的应力波传播研究
波动理论 | 细观非连续介质的应力波传播研究
-

波动理论 | 细观非均匀介质中的耦合波动传播
波动理论 | 细观非均匀介质中的耦合波动传播
-

波动理论 | 脆性梁弯曲断裂所激发的弯曲波
波动理论 | 脆性梁弯曲断裂所激发的弯曲波
-

波动理论 | 相变对TiNi 合金薄壁管中波速的影响
波动理论 | 相变对TiNi 合金薄壁管中波速的影响
-

波动实验与测试 | 基于广义波阻抗理论的SHPB 试验中弹性压缩阶段试件应力-应变曲线的应力波效应及其影响机理
波动实验与测试 | 基于广义波阻抗理论的SHPB 试验中弹性压缩阶段试件应力-应变曲线的应力波效应及其影响机理
-

波动实验与测试 | 多胞子弹冲击泡沫夹芯梁的动力学响应分析
波动实验与测试 | 多胞子弹冲击泡沫夹芯梁的动力学响应分析
-

波动实验与测试 | 霍普金森杆实验方法中材料弹性阶段杨氏模量及其曲线准确性分析
波动实验与测试 | 霍普金森杆实验方法中材料弹性阶段杨氏模量及其曲线准确性分析
-

波动实验与测试 | 基于摆锤加载岩杆SHPB 装置的充填体动态力学特性测试方法
波动实验与测试 | 基于摆锤加载岩杆SHPB 装置的充填体动态力学特性测试方法
-
学科相关 | 学科动态
学科相关 | 学科动态



















 登录
登录